2.       JEDNADŽBE GIBANJA I SILE U SUSTAVU TRUP-VIJAK-KORMILO

 

 

2.1       Jednadžbe gibanja i pridružene mase

 

2.1.1        Koordinatni sustavi i transformacije koordinata

 

Inercijalni koordinatni sustav  O₀ x₀ y₀ z₀  je nepomični pravokutni koordinatni sustav,

x₀            horizontalna koordinatna os usmjerena prema sjeveru,

y₀            horizontalna koordinatna os usmjerena prema istoku,

z₀            vertikalna koordinatna os usmjerena prema centru Zemlje.

 

Brodski koordinatni sustav  O x y z  je pravokutni koordinatni sustav kruto vezan za brod. Položaj ishodišta brodskog koordinatnog sustava  O  na brodu je, općenito, proizvoljan. Uobičajeno je, me|utim, da se za ravnine koordinatnog sustava izabiru slijedeće tri karakteristične, me|usobno okomite, ravnine:

Oxy         horizontalna ravnina projektne vodne linije broda

Oyz         vertikalna ravnina glavnog rebra

Ozx          vertikalna ravnina uzdužne simetrije broda

U tom slučaju se koordinatne osiju nazivaju:

x              uzdužnom, pozitivno usmjerenom prema prmcu,

y              poprečnom, pozitivno usmjerenom preko desnog boka,

z              vertikalnom, pozitivno usmjerenom prema dnu.

 

Položaj i orjentacija brodskog koordinatnog sustava  O x y z  spram inercijalnog  O₀ x₀ y₀ z₀  jednoznačno se mogu opisati pomoću slijedeće četiri veličine:

         radijvektor brodskog koordinatnog sustava

j              kut bočnog nagiba broda (ili kut valjanja) je nagib broda oko uzdužne osi x

q              kut trima broda (ili kut posrtanja) je nagib broda oko poprečne osi y

y             kut kursa broda (ili kut zaošijanja) je kut uzdužnice broda mjeren od pravca sjevera

 

Transformacija brodskog koordinatnog sustava u inercijalni odre|ena je vektorskom jednadžbom:

 

gdje su:

                              koordinate proizvoljne točke u brodskom koordinatnom sustavu

                             koordinate te iste točke u inercijalnom koordinatnom sustavu

                   koordinate ishodišta brodskog koordinatnog sustava

 

U matričnom obliku jednadžba transformacije ima oblik:

 

 

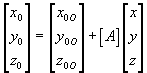
gdje je  ortogonalna matrica transformacije:

 

 

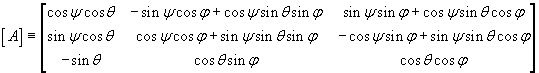
Inverzna transformacija:

 

,

 

 

provodi se pomoću izraza:

 

 

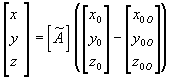
gdje je  transponirana matrica .

 

 

2.1.2        Brzina i ubrzanje proizvoljne točke broda

 

Gibanje broda može se smatrati superpozicijom translacije ishodišta O brzinom   i  rotacije oko ishodišta kutnom brzinom .

 

Ako se točka broda u brodskom koordinatnom sustavu nalazi na koordinati, u inercijalnom sustavu radijvektor točke će biti:

 

               

 

Derivacijom ovog izraza po vremenu dobiva se:

 

               

 

Lijeva strana ove jednadžbe predstavlja brzinu translacije točke gledane iz inercijalnog koordinatnog sustava:

 

               

 

Prvi član na desnoj strani predstavlja brzinu translacije ishodišta brodskog koordinatnog sustava gledanog iz inercijalnog koordinatnog sustava:

 

               

 

Budući da je radijvektor točke gledan iz brodskog koordinatnog sustava  vremenski nepromjenjiva vektorska veličina, njegova derivacija po vremenu nastaje samo zbog rotacije brodskog koordinatnog sustava spram inercijalnog, pa vrijedi:

 

               

 

Prema tome, brzina točke broda u inercijalnom koordinatnom sustavu odre|ena je izrazom:

 

 

Ubrzanje točke dobiva se deriviranjem brzine po vremenu:

 

  

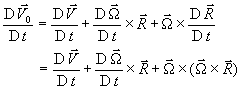
ili

 

gdje su:

                             ubrzanje točke broda gledano iz inercijalnog koordinatnog sustava i

                                     ubrzanja ishodišta brodskog koordinatnog sustava.

 

Jednadžbe za brzinu i ubrzanje u matričnom obliku poprimaju oblik:

 

 

 

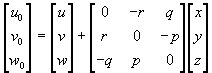
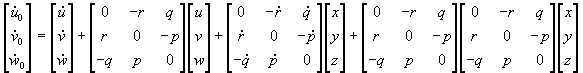
što nakon sre|ivanja daje:

 

 

 

 

 

 

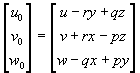
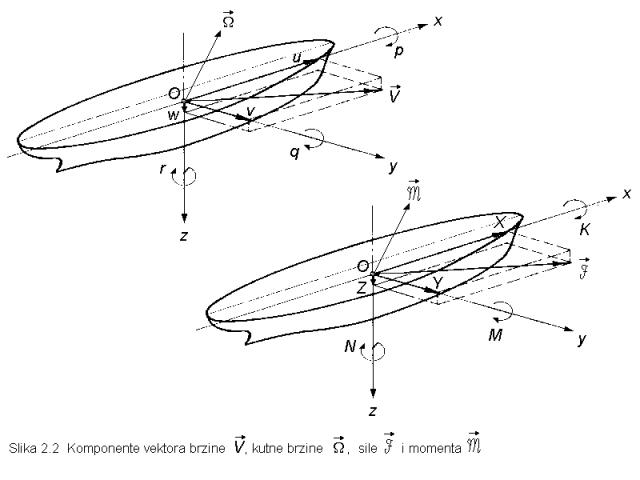
2.1.3        Opće jednadžbe gibanja broda

 

 

Gibanje broda pod djelovanjem sila  i momenata  opisuje se jednadžbama:

 

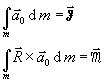
gdje su:

                              ubrzanje točke broda

                                     radijvektor točke broda

 

 

U matričnom obliku jednadadžbe gibanja glase:

 

 

 

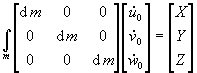
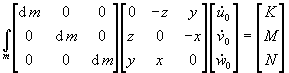
Uvrštenjem prethodno izvedenog izraza za ubrzanje:

 

 

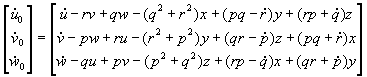
dobiva se:

 

 

 

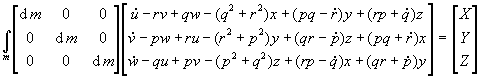
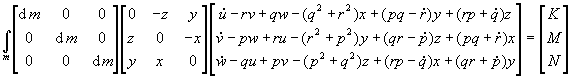
Korištenjem supstitucija:

 

 

gdje su:

                                                           masa broda

                           radijvektor težišta broda

 

nakon integracije dobiva se 6 općih jednadžbi gibanja broda kao krutog tijela:

 

 

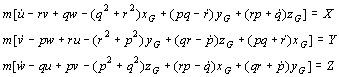
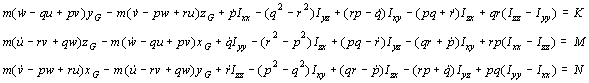
Ako je brod simetričan na koordinatnu ravninu Oxz, vrijedi , pa se gornje jednadžbe pojednostavljuju na oblik:

 

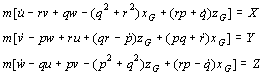
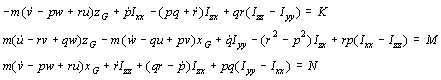
Ako se za ishodište brodskog koordinatnog sustava izabere težište broda,, jednadžbe poprimaju još jednostavniji oblik:

 

 

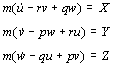
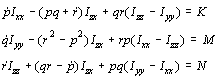
2.1.4        Jednadžbe gibanja broda u horizontalnoj ravnini

 

Pretpostavke:

1.  Brod je simetričan na koordinatnu ravninu Oxz, pa vrijedi

               

2. Utjecaj vertikalnih gibanja na horizontalna je zanemariv, pa se može staviti:

               

 

Uvrštenjem u opće jednadžbe gibanja dobiva se:

 

 

Ako se za ishodište brodskog koordinatnog sustava izabere težište broda,, jednadžbe poprimaju još jednostavniji oblik:

 

 

2.1.5        Pridružene mase

 

 

Odre|ivanje inercijalnih hidrodinamičkih sila koje djeluju na brod provodi se uz pretpostavku potencijalnog strujanja u neograničenoj, nestlačivoj, idealnoj tekućini.

 

Neka je  potencijal strujanja takav da zadovoljava slijedeće uvjete:

 

1)   Laplaceovu jednadžbu (kontinuiteta):

2)   Uvjet isčezavanja u beskonačnosti:

 

 

3)   Uvjet nepromočivosti stjenke broda S

 

                        na  S

 

gdje je  jedinični vektor normale na stijenku S.

 

 

Zbog linearnosti uvjeta slijedi da potencijal ima oblik sume potencijala komponentalnih gibanja:

 

 

 

Svaki pojedinačni potencijal zadovoljava sva tri navedena uvjeta.

 

Uvjeti nepromočivosti elementarnih potencijala imaju oblik:

 

 

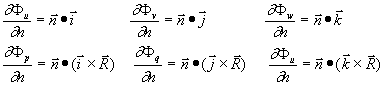
Budući da desne strane gornjih izraza ne ovise o vremenu, slijedi da niti lijeve strane ne mogu biti funkcije vremena. Prema tome, potencijali elementarnih gibanja ovise samo o obliku trupa broda.

 

Ako se uvedu slijedeće oznake:

 

 

potencijal poprima oblik:

 

 

Kinetička energija idealne, nestlačive tekućine u potencijalnom strujanju odre|ena je površinskim integralom:

 

               

Uvrštenjem potencijala u ovu jednadžbu može se dobiti:

 

ili

               

gdje je:

tzv matrica pridruženih masa.

 

U općem slučaju, matrica pridruženih masa sadrži 36 različitih veličina ovisnih o obliku tijela, obliku granica tekućine i načinu gibanja trijela. U slučaju gibanja tijela u neograničenoj tekućini matrica je dijagonalno simetrična, , pa se pojednostavljuje na 21 različiti član. Sva plovila su gotovo redovito simetrična spram uzdužne vertikalne ravnine O x z. U tom slučaju 18 članova matrice poprima vrijednost nula, pa se matrica pridruženih masa za gibanje tijela u neograničenoj tekućini svodi na 12 različitih članova, a izraz za kinetičku energiju poprima oblik:

 

 

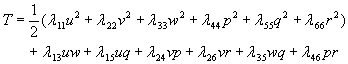
Poznato je da se projekcije vektora količine gibnja mogu dobiti deriviranjem kinetičke energije po odgovarajućim komponentama brzine:

 

            i = 1, 2, 3

Projekcije vektora momenta količine gibnja mogu se dobiti deriviranjem kinetičke energije po odgovarajućim komponentama kutne brzine:

 

                i = 4, 5, 6

 

Inercijalna sila kojim tekućina djeluje na trup, prema zakonu količine gibanja iznosi:

 

               

 

Inercijalni moment odre|uje se prema zakonu količine momenta gibanja:

 

               

 

Pri gibanju tijela s vertikalnom uzdužnom simetrijom u neograničenoj tekućini, za komponente inercijalne sile i momenta mogu se dobiti slijedeći izrazi:

 

 

 

 

 

 

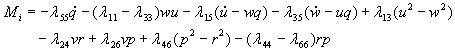
Dobivene jednadžbe koriste se za odre|ivanje inercijalnih sila kod analiza gibanja duboko uronjenih podvodnih plovila u dubokoj vodi (ili zrakoplova dovoljno udaljenih od tla). 

 

Kod analiza gibanja površinskih brodova u manevru utjecaj slobodne površine na inercijalne sile se redovito zanemaruje. Zbog toga se neporemećena slobodna površina vode može smatrati ravninom simetrije tzv. udvojenog trupa, a gibanje broda gibanjem udvojenog trupa u neograničenoj tekućini. Za gibanje takvog trupa u gornje jednadžbe se može uvrstiti:

 

  

 

pa se za inercijalne sile kod gibanja površinskog broda dobivaju slijedeći izrazi: 

 

 

Za analize kod kojih se gibanje broda može smatrati ravninskim gibanjem u horizontalnoj ravnini, tj.:

 

 

dobivaju se slijedeće 3 jednadžbe:

 

 

 

2.1.6        Kvazistacionarne jednadžbe gibanja broda u horizontalnoj ravnini

 

 

Sile na desnim stranama jednadžbi gibanja broda u horizontalnoj ravnini (izvedene u 2.1.4):

 

 

mogu se, bez gubitka na općenitosti, prikazati u obliku suma inercijalnih i preostalih komponenata:

 

 

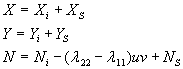
pa će, nakon uvrštenja izraza za inercijalne sile (iz 2.1.5), jednadžbe gibanja poprimiti oblik:

 

 

Nakon sre|ivanja se dobiva:

 

 

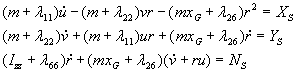
Uvo|enjem supstitucija:

 

               

 

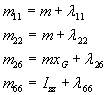
dobiva se konačno:

 

 

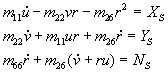
Kada bi se u gornjim jednadnadžve uvrstilo  dobile bi se opće jednadžbe ravninskog gibanja dvostruko simetričnog krutog tijela pod djelovanjem sila i  te momenta .

 

Prema tome, inercijalne hidrodinamičke sile koje nastaju zbog gibanja tijela u vodi djeloju na tijelo tako kao da povećavaju inercijalne značajke njegove mase. Zbog toga se veličine  nazivaju pridruženim ili dodatnim masama.

 

Kako su, sada, inercijalne komponente prebačene na lijevu stranu jednadžbi gibanja, na desnim stranama su  ostale sve druge sile neinercijalnog porjekla. Drugim riječima, desne strane dobivenih jednadžbi gibanja ne ovise eksplicite o ubrzanjima ,  i .

 

Prema tome, veličina silai  te momenta u nekom trenutku t  ovist će, izme|u ostaloga, o trenutnim vrijednostima komponentata brzina u, v  i r,  neovisno o tome kako su postignute, i jednake su onim veličinama sila i momenta koje bi djelovale na brod pri njegovom ustaljenom (stacionarnom) kruženju istim tim brzinama. 

 

Ovaj zaključak je, naravno, valjan u okvirima teorijskih pretpostavki. U realnim uvjetima desne strane izvedenih jednadžbi gibanja ovise i o ubrzanjima. Iskustvo pokazuje, me|utim, da su preostale inercijalne hidrodinamičke komponente sila klasičnih površinskih brodova vrlo male u odnosu na inercijalne sile mase broda i inercijalne sile pridruženih masa.

 

Zbog toga, a s ciljem mogućnosti rješavanja dobivenih diferencijalnih jednadžbi, uvodi se hipoteza kvazistacionarnosti koja pretpostavlja da su trenutne vrijednosti svih preostalih hidrodinamičkih sila jednake onima koje bi djelovale na brod da je u stacionarnom kruženju. Dobivene jednadžbe se stoga nazivaju kvazistacionarnim jednadžbama gibanja broda.

 

 

2.1.7        Odre|ivanje pridruženih masa

 

 

Za proračun pridruženih masa po izvedenim formulama potrebno prvo proračunati potencijale strujanja oko broda. Budući da je proračun potencijala strujanja oko broda kao trodimenzionalnog tijela često nepraktičan pristup, za odreživanje pridruženih masa koriste se slijedeći praktični postupci:

 

1.        proračun pomoću empirijskih formula

2.        proračun približnim metodama

3.        modelska ispitivanja

 

Empirijskie formule treba vrlo oprezano koristiti. Uvijek treba provjeriti za koji su tip trupa broda i koje područje omjera glavnih dimenzija broda su razmatrane formule dobivene.     

 

Najčešće korištena približna metoda je metoda kriški s empirijskim korekcijama. Pridružene mase trodimenzionalnog trupa broda računaju se integracijom dvodimenzionalnih pridruženih masa presjeka preko duljine broda po formulama:

 

 

 

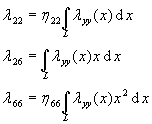
gdje je   pridružena masa zanošenja beskonačno dugačkog cilindra čiji je poprečni presjek jednak poprečnom presjeku broda na koordinati x. Za odre|ivanje dvodimenzionalnih pridruženih masa koriste se jednostavniji teorijski postupci. U praksi se često stvarni brodski presjeci zamjenjuju geometrijski ekvivalentnim matematičkim formama (npr. Lewisove forme) za koje postoje i tablice pridruženih masa.

 

Koeficijenti   i   su iskustveni ispravci zbog trodimenzionalnosti trupa. Prema Pabstu:

 

  

 

 

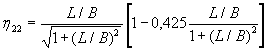
Metodom kriški dobivaju se pouzdaniji podaci od empirijskih formula, no nije moguće izračunati priduženu masu za uzdužno ubrzano gibanje broda .

 

Eksperimentalno odre|ivanje pridruženih masa broda danas se najčešće provodi ispitivanjem modela broda na  ure|aju za prisilno oscilatormo gibanje modela PMM (Planar Motion Mechanism).

 

PMM se sastoji od dva oscilatora, od kojih jedan proizvodi poprečne oscilacije na pramcu, a drugi poprečne oscilacije na krmi, dok se model tegli konstantnom brzinom u₀. (Indeks 0 govori da se radi o komponenti brzine inercijalnom koordinatnom sustavu).

 

Dva dinamometra postavljena u točkama B i S, mjere poprečne sile Y_S i Y_B potrebne za prisilno oscilatorno gibanja modela.

 

 

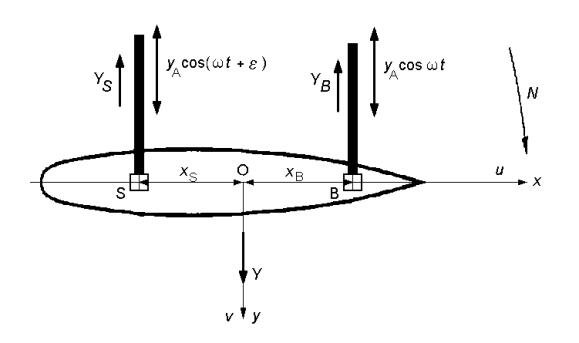
Slika 2.3  Shema ispitivanja modela na PMM

 

Sile koje djeluju na model u ravnoteži su sa silama prisilnog vo|enja modela, pa vrijedi:

 

 

Pomoću mehanizma model se prisilno dovodi u poznato stanje gibanja. Dakle, prilikom ispitivanja poznate su

 

1.        vremenske funkcije komponenata ravninskog gibanja modela:           u(t), v(t) i r(t)       

2.       vremenske funkcije sila:                                                                                              X(t), Y(t), N(t)

3.       inercijalne karakteristike modela:                                                                               m, I_zz, x_G

               

Uvrštenjem ovih funkcija u jednadžbe gibanja broda u horizontalnoj ravnini:

 

 

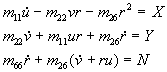
mogu se dobiti nepoznate konstante: m₁₁, m₂₂, m₂₆, m₆₆,

 

a iz njih, na kraju, pridružene mase:

 

Ako se pokus provede tako da se model dovede u jednostavno harmonijsko gibanje po sinusoidalnom zakonu jednadžbe gibanja postaju jednostavne funkcije iz kojih se nepoznate konstante mogu odrediti analitički. Na slici 2.4 shematski su prikazana dva najvažnija tipa pokusa: gibanje modela bez zaošijanja (r = 0) i gibanje modela bez zanošenja (v = 0) .

 

Oscilatorno gibanje mora imati velike amplitude pomaka (zastajkivanja, zanošenja ili zaošijanja) i velike periode gibanja kako bi se smanjio utjecaj generiranja valova na slobodnoj površini.

 

 

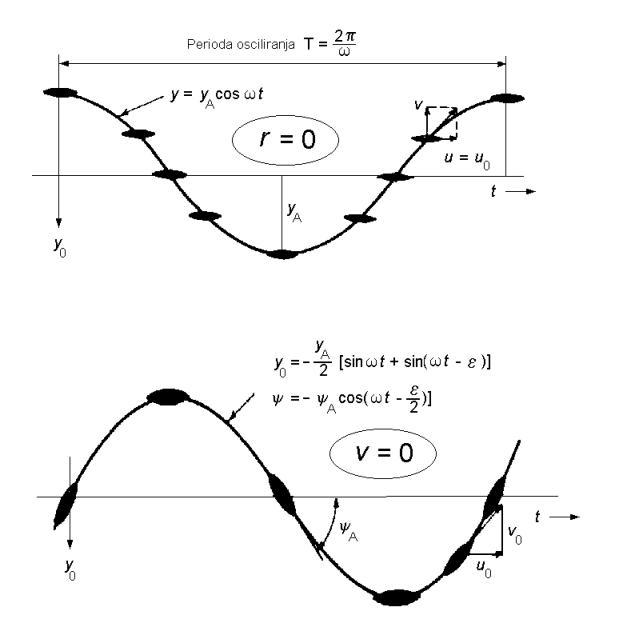
Slika 2.4                  Oscilatorno gibanje modela pri ispitivanju na PMM

                                gore:       zanošenje bez zaošijanja

                                dolje:      zaošijanje bez zanošenja