3.2.Tehnike modelskih ispitivanja s vezanim modelom

 

Ispitivanja s vezanim modelom izvode se korištenjem mehanizama s planarnim gibanjem ili korištenjem rotirajuće konzole. Pri obje tehnike model se ispituje unutar kompletnog raspona interesantnih varijabli, kao što su kut trima, ubrzanja zaošijanja, ubrzanja zanošenja, broj okretaja propelera i kut otklona kormila, a rezultati se analiziraju da bi se dobili hidrodinamički koeficijenti potrebiti u jednadžbama gibanja.

Za ove pokuse potrebno je poznavati linearne koeficijente, tj.derivacije po brzini Y_V i N_{V .} Za brod na bilo kojem gazu i trimu mogu se odrediti u standardnom bazenu teglenjem balastiranog modela konstantnom brzinom, na odgovarajućem Froudeovom broju broda, s različitim kutevima kursa b modela, tkzv pokusi kosog tegljenja (oblique towing tests).

Vidi se da brzinu u y smjeru dobivamo kao : v = -Vsinb ( minus predznak je zbog konvencije o pozitivom smjeru).

Dinamometar, postavljen u ishodištu O mjeri silu Y i moment N za sve kuteve b modela. Rezultati ovih mjerenja crtaju se kao funkcija brzine v, a nagib krivulje za vrijednost v = 0, daje numeričku vrijednost  Y_V i N_V, za model. Te vrijednosti se izražavaju u bezdimenzionalnom obliku, pa se rezultati za brod dobivaju množenjem s odgovarujćim brodskim vrijednostima.

Ova ispitivanja uobičajeno se izvode s realnim režimom radom propelera i kormilom u neutralnom položaju, a smještaj dinamometra ne mora nužno biti u težištu sistema( ali se u tom slučaju mora još raditi korekcija za težište).

Ovakvo ispitivanje može se koristiti za određivanje vrijednosti Y_d i N_d , tako da kut kursa modela b bude jednak 0, a teglenje modela izvodi se s različitim kutevima otklona kormila  d_R. Mjerenja tada daju silu Y i moment N  kao funkciju kuta otklona kormila, i crtanjem obje vrijednosti kao funkcije kuta otklona kormila dobivamo za d = 0, iznose Y_d i N_d .Usporedba vrijednosti Y_d i N_dd_R dobivenih ovakvim ispitivanjem daju veličinu interaktivnih efekata kormila i trupa.

Test održavanja ravnog kursa može se koristiti i za određivanje utjecaja v na Y_V, te (N_d , d_R) na  (Y_V ,N_V), što su vrlo značajni podaci za nelinearnu teoriju.

3.2.1     Modelska ispitivanja vezanog modela na rotirajućoj  konzoli

 

 

Ova tehnika mjerenja vrijednosti Y_R i N_R zahtijeva okrugli bazen i posebne uređaje, tzv. rotirajuća konzola, prikazan na slici.

Kutna brzina se kod ovakvog ispitivanja narine modelu, tako da se model fiksira na kraj poluge i rotira zajedno s rotirajućom konzolom oko vertikalne osi postavljene u središtu bazena ( slika 2.2.2.). Model je orijentiran tako da su njegove x i z osi, okomite na radijalnu polugu, a učvršćen je za polugu na polovici svoje duljine, pa kao rezultat ovakvog položaja, model rotira oko osi bazena na radijusu r, dok je njegova brzina u poprečnom smjeru v cijelo vrijeme jednaka 0 (b=0), a aksijalna komponenta brzine u₁ jednaka je njegovoj linearnoj brzini. Model se rotira s konstantnom linearnom brzinom na različitim radijusima R, a dinamometar mjeri silu Y i moment N koji djeluju na model. Obzirom da je kutna brzina r dana izrazom r = u₁ / R, jedini način za variranje kutne brzine r , uz konstatnu linearnu brzinu u₁, je variranje radijusa R. Vrijednosti Y_r i N_r dobivaju se očitavanjem iz dijagrama za vrijednost r = 0.

Za razliku od rezultata ispitivanja Y_v i N_v, rezultati ovog pokusa su ovisni o položaju težišta modela, koji mora biti na istom mjestu kao i kod broda. Ovom tehnikom mogu se ispitivati i Y_v i N_v, kao i Y_r i N_r . To se postiže teglenjem modela na različitim kutevima b za svaku vrijednost kutne brzine r. Rezultati za Y_d i N_d mogu se dobiti na potpuno analogan način kao i Y_v i N_v . Nažalost, vrijednosti dobivene za Y_v i N_v , te Y_d i N_d ovim ispitivanjem nisu identični rezultatima iz pokusa održavanja ravnog kursa.

Za rješavanje nelinearne teorije, tehnika ispitivanja na rotirajućoj konzoli osigurava vrijednosti hidrodinamičkih sila i momenata za velike vrijednosti v, r, d_r, a isto tako daje i potrebne informacije o sprezi ova 3 parametra. [toviše, uz dovoljan broj mjernih uređaja na konzoli, može se mjeriti i X sila i moment ljuljanja K, kao funkcija od v, r, d_r . Oni su potrebni u nelinearnoj teoriji za predviđanje gubitka brzine i naginjanju broda tijekom manevra. Ako se model, vezan na kraju konzole, ispituje na različitim kutevima nagiba f za različite vrijednosti v, r, d_r,mogu se dobiti nelinearni efekti nagibanja i efekti interakcije između  f, v, r, d_r.

Problemi tehničke naravi koji se javljaju kod ove tehnike ispitivanja su:

·      veličina bazena (ne može se izvoditi u bazenima koji se uobičajeno koriste za ispitivanje otpora i propulzije)

·      model mora biti ubrzavan tako da se rezultati snime pri istom okretu, jer se inače model giba u vlastitom sustrujanju, pa nije moguće tada odrediti  brzinu modela u odnosu na okolni fluid

·      da bi se odredile vrijednosti Y_r i N_r te Y_v i N_v  za vrijednost r = 0, potrebni su podaci dobiveni sa što manjom kutnom brzinom r što iziskuje veliki R (radijus bazena) i što veći model

 

 

3.2..2.      Tehnika modelskog ispitivanja s mehanizmom za planarno gibanje (PMM)

 

PMM pokusi razvijeni su u HSBM, međutim ITCC je standardizirao način izvođenja pokusa. Kao standardi prihvaćene su slijedeće konvencije:

1. PMM pokusi se mogu izvoditi za poniranje, posrtanje i ljuljanje modela.

2. Svi referentni pokusi izvode se s potpuno opremljenim modelom, i propelerom koji radi u realnom režimu (točka ship - propulsion)

3. Sile i momenti mjere se u odnosu na koordinatni sustav modela, s ishodištem u X_G (uzdužni položaj težišta sustava).

Uobičajeno, kompletan program ispitivanja ovisi o tipu broda,potrebnim informacijama i samoj fazi projekiranja. Kompletan program trebao bi davati sve podatke o manevarskim karakteristikama u dubokoj vodi, što znači da mora uključivati slijedeća ispitivanja:

1. Otpor i propulzija s potpuno opremljenim modelom za prognoziranje EHP, SHP, RPM kao funkcije brzine za prototip broda u pravom mjerilu.

2. PMM testove s golim trupom, da bi se dobile informacije o promjenama različitih projekata kormila

3. Osnovni (referentni) PMM pokusi izvode se samo u točki propulzije s potpuno opremljenim modelom za analizu početne stabilnosti i kontrolnih karakteristika za preliminarni projekt  autopilota

4. Standardni PMM pokusi (uključujući i overload i underload) osiguravaju komplentan skup hidrodinamičkih koeficijenata (iz matematičkog modela) potrebitih za kompjutorsku simulaciju proračuna upravljivosti za određeni brod.

Ukoliko se radi o postojećem brodu, ili projektu s fiksnim hidrodinamičkim projektom (forma, propulzija), izvode se samo pokusi 3 i 4.

Izvođenje referentnog PMM pokusa (za svaki od tri osnovna načina gibanja) broj okretaja propelera modela odgovara broju okretaja propelera u naravi uz kut kormila  i “drift” kut  (kut napredovanja).

Model se tegli na konstantnoj brzini, tako da se njegovo težište sustava kreće pravocrtno s diskretnim promjenama kuta napredovanja koji se drži konstantnim tijekom jedne vožnje. Vrijednosti kuta b određuju se prije svake vožnje tako da se pokrije odabrani raspon, s inkrementom od 2⁰, ili većim, ovisno o tipu broda. Mjere se komponente sile Y₁, Y₂ ,X₁,X₂.

3.2.2.1. Čisto bočno ljuljanje

 

Model se tegli na konstantnoj brzini i istovremeno oscilira, tako da je njegova uzdužna simetralna ravnina uvijek paralelna s putanjom kolica, a težište sustava opisuje sinusoidalnu putanju. Takvo gibanje postiže se osciliranjem “swaying carriage” na zadanoj frekvenciji i amplitudi pomoću servo-kontrolnog sustava. Željeni raspon postiže se variranjem amplitude oscilatorne frekvencije, ili kombinioranjem oba parametra. Svaka vožnja izvodi se konstantnom brzinom kolica, a oscilatorna frekvencija i amplituda drže se konstantnima tijekom mjerenja.

3.2.2.2. Čisto zaošijanje

 

Dok se model tegli konstantnom brzinom, istovremeno oscilira tako da je njegova uzdužna simetralna ravnina uvijek tangencijalna na putanju težišta sustava (sinusoidalna putanja). Izvođenje pokusa je isto kao i kod čistog ljuljanja.

3.2.2.3. Opis PMM pokusa

 

Mehanizam za planarno gibanje razvijen je da bi se izbjegli troškovi ispitivanja na rotirajućoj konzoli, te da bi se za određivanje vrijednosti Y_v i N_v  mogli koristiti bazeni u kojima se ispituju i otpor i propulzija, a isto tako da bi se mogle odrediti derivacije po kutnoj brzini r: Y_r i N_r, isto kao i derivacije po akceleracijama:.

PMM se sastoji od dva oscilatora, od kojih jedan proizvodi poprečne oscilacije na pramcu, a drugi poprečne oscilacije na krmi, dok se model giba konstantnom brzinom u₀ po središnjici bazena. (Indeks 0 koristi se zbog toga što se brzina mjeri duž osi vezane za zemlju, tj. uzdužne osi x₀ koja odgovara središnjici bazena).

 

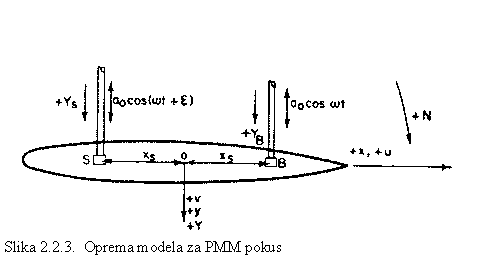
Dva dinamometra postavljena u točkama B i S (Slika 2.2.3.), mjere oscilatornu Y silu, koja je rezultat zanošenja modela bez zaošijanja.  Oscilacije zanošenja dane su u formi:

y₀ = y = a₀coswt,              

a derivacije po brzini Y_v i N_v dobivaju se prema slijedećim relacijama:

Y_v =

i analogno za N_v:

N_v =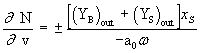

 

Index  “out” se odnosi na amplitude Y_B i Y_S mjerene s pomakom u fazi za 90⁰ u odnosu na Y₀.

Da bi se pomoću PMM odredile vrijednosti Y_r i N_r,  mjerenje se mora izvoditi za tako da bi se dobile kutna brzina i akceleracija pri , model se mora tegliti tako njegova uzdužna os x, uvijek bude tangencijalna na putanju modela.

 

 

 

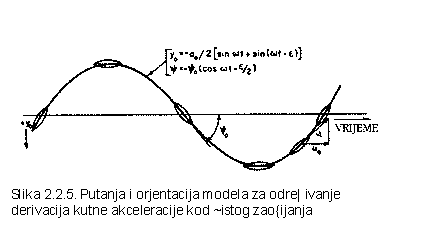
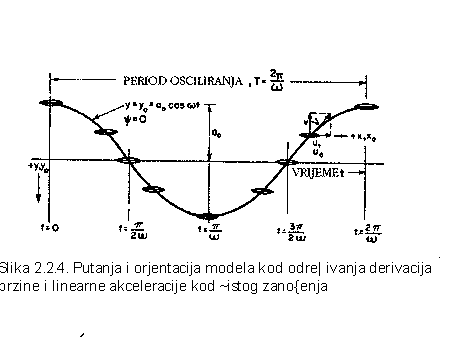
Na slici 2.2.5. prikazano je čisto zaošijanje.

Rezultati PMM ispitivanja ovisni  su: o masenom momentu inercije, radijusu okreta i x_G . Potrebito je napomenuti da se model mora balastirati na odgovarajući gaz i trim, mora biti potpuno opremljen za vlastiti pogon, s kormilom u neutralnom položaju. Obzirom da oscilatorna gibanja proizvode valove, čije karakteristike ovise o frekvenciji sistema valova,mora se  PMM-om odrediti ovisnost derivacija o frekvencijama. Za mnoge probleme iz upravljivosti  najzanimljivije su niske frekvencije ili čak s frekvencijom jednakom 0, pa da bi odredili tražene derivacije rezultati pokusa se prikažu dijagramom derivacija-frekvencija i ekstrapoliraju se za vrijednost frekvencije jednaku 0.

Treba naglasiti da derivacije dobivene pokusom održavanja kursa i pokusom s rotirajućom konzolom odgovaraju frekvenciji 0. Te vrijednosti odgovaraju rezultatima PMM ekstrapolirane na vrijednost frekvencije 0 .