4.2       Opća rješenja lineariziranih jednadžbi

 

 

Jednadžbe (4.6) su nehomogene linearne jednadžbe s konstantnim koeficijentima za koje je poznato da se opće rješenje jednadžbi može prikazati u obliku superpozicije rješenja homogenih jednadžbi i partikularnih rješenja nehomogenih jednadžbi, dakle:

 

                                                                                                                                        (4.8)

 

Rješenja homogenih jednadžbi imaju oblik:

 

                                                       

                                                                                                                                                  (4.9)       

 

gdje su   r₁ , r₂ , v₁  i v₂ konstante integracije ovisne o početnim uvjetima, a s₁  i s₂  su korjeni karakteristične algebarske jednadžbe:

 

 

do kuda slijedi:

 

 

pa se za rješenja homogenih jednadžbi dobiva:

 

                                                 

                                                                                                                                               (4.10)

 

Partikularna rješenja jednadžbi ovise o obliku vremenske funkcije otklona kormila. Ako se funkcija otklona prikaže u linearnom obliku:

 

                                                                                                                                            (4.11)

 

partikularna rješenja poprimaju oblik:

 

                                                                                                       (4.12)

 

Uvrštenjem  (4.10)  i  (4.12)  u  (4.8)  dobivaju se opća rješenja lineariziranih jednadžbi gibanja za slučaj linearne promjene kuta otklona kormila (4.11)  u obliku:

 

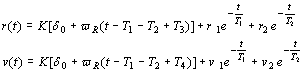                                                                       (4.13)