4.3       Formula za proračun kursa broda

 

 

Uvođenjem supstitucije:

 

                                                                                                                                                                              (4.14)

 

opće rješenje za kutnu brzinu  u  (4.13)  poprima oblik:

                                                                                           (4.15)

 

Ovaj izraz sadrži dvije nepoznate konstante integracije, r₁   i  r₂ , koje ovise o početnim uvjetima. Općenito rješenje konstanti integracije dobit će se ako se omogući da brod u početnom trenutku vremena  ima proizvoljno gibanje s trenutnom kutnom brzinom  i trenutnim kutnim ubrzanjem , tj:

               

                                                                                                                                                                           (4.16)

 

Deriviranjem (4.15) po vremenu dobiva se izraz za kutnu brzinu:

 

                                                                                                                (4.17)

 

Uvrštenjem početnih uvjeta  (4.16)  u (4.15) i (4.17) i rješenjem po r₁ i r₂ dobiva se:

 

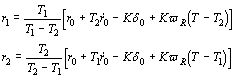                                                                                                                             (4.18)

 

Vremenska promjena kursa broda dobiva se po definiciji:

 

                                                                                                                                                               (4.19)

 

Ako, općenito, u početnom trenutku vremena brod plovi u početnom kursu

 

                                                                                                                                                                       (4.20)

 

integracijom  (4.15)  po vremenu dobiva se:

 

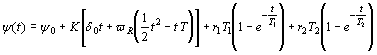                                                                              (4.21)

 

Ako su poznate hidrodinamičke značajke sustava trup-vijak-kormilo (4.3) moguće je izračunati konstante broda kao linearnog sustava (4.7) i (4.14). Najčešće se pretpostavlja da u manevru sudjeluju samo hidrodinamičke sile trupa i kormila, pa će gradijenti sila biti sume:

 

                                    

 

 

Odabiranjem ili određivanjem početnih uvjeta (4.16) i (4.20) određene su i konstante integracije (4.18) čime su, konačno, potpuno određene i formule za proračun kutne brzine (4.15), kutnog ubrzanja (4.17) i kursa broda (4.21).

 

Svaka vremenska funkcija otklona kormila  može po želji dovoljno točno opisati poligonalnom krivuljom, dakle neprekinutim nizom linearnih segmenata.

 

Na početku prvog segmenta brod se nalazi u poznatom stanju, najčešće u ustaljenom ravnocrtnom gibanju brzinom u₀ s kormilom u sredini:

 

                 

 

Tijekom prvog segmenta koji završava u trenutku , kormilo se okreće na kut , konstantnom brzinom :

                  

 

Unutar vremenskog intervala , primjenom formula (4.15), (4.17)  i  (4.21) moguće je izračunati  vrijednosti funkcija. Vrijednosti ovih funkcija na kraju intervala postaju početne vrijednosti za drugi segment funkcije otklona kormila, tj.

 

iz prvog segmenta 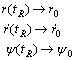 za drugi segment

 

Drugi segment računa se dalje jednako kao prvi segment, pri čemu se vrijeme  t  unutar drugog segmenta mjeri od početka segmenata - a ne od početka pokusa !

 

Opisanim postupkom moguće je proračunati osnovne parametre Z-manevra dinamički stabilnih brodova. Pouzdanost proračuna ovisit će o pouzdanosti ulaznih podataka - hidrodinamičkih koeficijenata (4.3). Modeliranje i određivanje hidrodinamičkih značajki sustava trup-vijak kormilo čini osnovni problem kompletnog područja upravljivost kao grane hidrodinamike broda..