4.4       Dinamička stabilnost kursa

 

 

Primjenom općih rješenja lineariziranih jednadžbi gibanja broda u horizontalnoj ravnini (4.13):

 

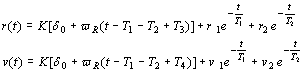
mogu se izvesti uvjeti dinamičke stabilnosti kursa broda kako slijedi.

 

Ako u nekom trenutku t = 0, brod kruži s kutnom brzinom

 

               

 

nakon prestanka djelovanja poremećajnih sila i povratka kormila u sredinu:

 

                 

 

vremenske funkcije kutne brzine i brzine zanošenja poprimit će oblik homogenog rješenja linearnog sustava:

 

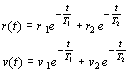                                                                                                                                 (4.22)

 

 

Budući da su , kako je pokazano, konstante ovisne o hidrodinamičkim značajkama broda i početnim uvjetima, brod će se stabilizirti u ravnocrtnom gibanju bez kruženja i zanošenja,

 

               

               

 

i u ravnom kursu

 

               

 

samo ako su obje konstante T₁ i T₂  pozitivne. Kada bi i samo jedna konstanta T₁ ili T₂  bila negativna odgovarajući eksponent u (4.22) postao bi pozitivan, pa bi obje jednadžbe divergirale: 

 

               

               

 

Prema tome, uvjet dinamičke stabilnosti broda može se napisati u obliku:

 

                T₁T₂  >  0

tj.

                                                                                       (4.23)

 

Brojnik gornjeg izraza uvijek je pozitivna veličina. Naime, jasno je da su masa m  i moment inercije I_z  pozitivne veličine. Fizikalno je jasno da su gradijenti sila po ubrzanju vlastitoga smjera () uvijek negativne veličine. Nadalje, koeficijenti međuutjecaja (), koji mogu biti pozitivni ili negativni (ovisno o nesimetriji pramac-krma), redovito su bitno manjih apsolutnih vrijednosti od koeficijenata vlastitih smjerova, pa je drugi član u brojniku gotovo zanemariv u odnosu na prvi. Prema tome, budući da je brojnik gornje jednadžbe uvijek pozitivan, razlomak će biti pozitian samo ako je i nazivnik pozitivan, tj :

 

                                                                                                        (4.24)

 

što se može napisati i u obliku:

 

                                                                                                                                        (4.25)

 

Ako se uvedu oznake:

 

                                                                                                                                                        (4.26)

gdje su: 

                x_v            krak prekretne sile nastale zbog zanošenja broda i

                x_r             krak prigušne sile nastale zbog početka kruženja broda.                  

 

uvjet dinamičke stabilnosti broda poprima oblik:

 

                                                                                                                                                             (4.27)

 

Dakle, uvjet dinamičke stabilnosti kursa broda može se izraziti riječima: Brod je dinamički stabilan u kursu ako mu je krak prigušne sile veći od kraka prekretne sile.